VHDL Episode 2 - A full adder
Previous episodes:
Going further with our VHDL tutorial, I think the code for today won’t fit anymore in your screen… On the other hand, this episode brings exciting news \o/ Today we are going to write and test an n-bit adder, i.e, an adder that’s able to add arbitrarily-sized binary numbers. The picture below illustrates the exact architecture we are going to implement, a “ripple-carry” adder:
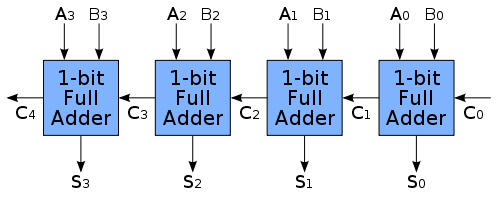
Only by looking at this picture you already notice this episode’s most important concept: the hierarchical modelling of hardware, using components. Which means we’ll define the architecture of an n-bit adder using a simpler, already defined component, the 1-bit adder of the last episode. Of course we have other concepts to introduce, but let’s first take a look at the code :)
library ieee;
use ieee.std_logic_1164.all;
entity nBitAdder is
Generic(nBits : integer := 8);
Port(
a : in std_logic_vector(nBits-1 downto 0);
b : in std_logic_vector(nBits-1 downto 0);
s : out std_logic_vector(nBits downto 0));
end nBitAdder;
architecture arch of nBitAdder is
component fullAdder is
Port(
a : in std_logic;
b : in std_logic;
cin : in std_logic;
s : out std_logic;
cout : out std_logic);
end component fullAdder;
for leftmost: fullAdder use entity work.fullAdder;
for rightmost: fullAdder use entity work.fullAdder;
constant N_BITS : integer := nBits;
signal sig_carryChain : array(1 to N_BITS-1) of std_logic;
begin
-- rightmost bit
rightmost: fullAdder
port map(
a => a(0),
b => b(0),
cin => '0',
s => s(0),
cout => sig_carryChain(1));
-- middle bits
middle: for i in 1 to N_BITS-2 generate
adder: fullAdder
port map(
a => a(i),
b => b(i),
cin => sig_carryChain(i),
s => s(i),
cout => sig_carryChain(i+1));
end generate middle;
-- leftmost bit
leftmost: fullAdder
port map(
a => a(N_BITS-1),
b => b(N_BITS-1),
cin => sig_carryChain(N_BITS-1),
s => s(N_BITS-1),
cout => s(N_BITS));
end arch;This nBitAdder has something new right in its entity section: The declaration of generic parameters. Those parameters declared under Generic have their value defined at synthesis-time, which means they are a sort of “offline” configuration. Different values for these parameters change the synthesis process, and result in actually different circuits. Several useful design decisions can be taken by only changing these generic parameters, but for now what we want is simple: we want to have an adder with generic-sized input and output ports.
Now for our adder’s port declaration:
Port(
a : in std_logic_vector(nBits-1 downto 0);
b : in std_logic_vector(nBits-1 downto 0);
s : out std_logic_vector(nBits downto 0));It now has only two input ports, the two numbers to be added, each represented by nBits bits. Each input port’s type is std_logic_vector, as already seen in the past episode… This time, however, the output port has size (nBits+1). This, of course, because the sum of two numbers with n bits each can possibly result in an extra carry bit :)
This design’s architecture section brings new concepts right away: the declaration of the component we are using, in this case a fullAdder. This sort of “LEGO-like” modelling, which uses simpler components to build more complex ones, is known as “bottom-up” engineering, and is a very popular hardware design methodology. A component declaration is nothing more than a COPY of the component’s entity section, substituting the entity keyword for component. Doing this seems repetitive, and indeed it is. There are ways to avoid this repetition, but these will come later in the tutorial. For now, let’s focus on the design itself…
The N_BITS constant is not strictly necessary, but it adds to the clarity of the code, and I’m also using it here to SHOW how constants can be used… On the following line comes the declaration for signal sig_carryChain. As we are using n fullAdders, n-1 wires are needed to interconnect their carry inputs and outputs. That’s why we declared an array of std_logic signals:
signal sig_carryChain : array(1 to N_BITS-1) of std_logic;The array’s indices range from 1 to N_BITS-1, and therefore it has N_BITS-1 elements, each element with type std_logic.
Let’s now actually “build” our LEGO model. We do this by instantiating the components, telling to which signal each port should be connected. First we instantiate the “rightmost” fullAdder, all others will be instantiated similarly.
rightmost: fullAdder
port map(
a => a(0),
b => b(0),
cin => '0',
s => s(0),
cout => sig_carryChain(1));The first bit (index 0) in the resulting sum is the rightmost bit, the least significant one. We connect this first fullAdder’s inputs to the first inputs of our nBitAdder, the output with the first output and we also connect the first fullAdder’s carry output to the first signal in our carry chain. In a similar way we also instantiate the most significant bit, the leftmost one. The only difference is that the last fullAdder’s carry output is connected to the “extra” (index N_BITS) bit in the resulting sum.
To instantiate the intermediary bits we need a more “flexible” approach :) We need, in fact, to instantiate N_BITS-2 more fullAdders. It is exactly this sort of “controlled repetition” that the generate construct allows.
middle: for i in 1 to N_BITS-1 generate
adder: fullAdder
port map(
a => a(i),
b => b(i),
cin => sig_carryChain(i),
s => s(i),
cout => sig_carryChain(i+1));
end generate middle;Each fullAdder has its inputs and outputs connected to the correspondingly indexed inputs and outputs in the n-bit entity. The carry input comes from the corresponding signal in the carry chain, and the carry output goes to the next signal in this chain. Everything matches as it should…
In terms of coding style this episode brings no big news! We just showed today how one can express comments in VHDL. In VHDL, you can only have single-line comments: every line beginning with -- (two consecutive minus signs) is ignored by the parser and considered a comment.
And now… for the truly important part of the episode: showing that the adder works, using a testbench! Well, this time the code for the adder itself was big, but incredibly enough the testbench became smaller, due to the usage of arrays, our new best friends in VHDL…
library ieee;
use ieee.std_logic_1164.all;
entity nBitAdder_testbench is
end nBitAdder_testbench;
architecture arch of nBitAdder_testbench is
component nBitAdder is
Generic(nBits : integer := 8);
Port(
a : in std_logic_vector(nBits-1 downto 0);
b : in std_logic_vector(nBits-1 downto 0);
s : out std_logic_vector(nBits downto 0));
end component nBitAdder;
for dut: nBitAdder use entity work.nBitAdder;
constant N_BITS : integer := 4;
signal sig_a : std_logic_vector(N_BITS-1 downto 0);
signal sig_b : std_logic_vector(N_BITS-1 downto 0);
signal sig_s : std_logic_vector(N_BITS downto 0);
type testInputArray is array(0 to 7) of std_logic_vector(N_BITS-1 downto 0);
type testOutputArray is array(0 to 7) of std_logic_vector(N_BITS downto 0);
constant testInputsA : testInputArray := (
"0000", "0001", "0100", "0101", "1000", "1001", "1100", "1101");
constant testInputsB : testInputArray := (
"1101", "1100", "1001", "1000", "0101", "0100", "0001", "0000");
constant testOutputs : testOutputArray := (
"01101", "01101", "01101", "01101", "01101", "01101", "01101", "01101");
begin
dut: nBitAdder
generic map(nBits => N_BITS)
port map(
a => sig_a,
b => sig_b,
s => sig_s);
tb: process
begin
for i in 0 to 7 loop
sig_a <= testInputsA(i);
sig_b <= testInputsB(i);
wait for 10 ns;
assert (sig_s = testOutputs(i)) report "fail" severity failure;
end loop;
assert false report "All tests passed." severity failure;
end process;
end arch;That’s it! Our testbench is only that large! And it works beautifully!
As always, please grab the code in this little package here: VHDL2 and fiddle with it. Compile the testbench, run and confirm that it works. Use GTKWave to surf the waveforms :P Once more, the included Makefile should help you with these tasks…
