VHDL Episódio 2 - Some quantos bits quiser
Episódios anteriores:
Continuando o tutorial de VHDL, dessa vez acho que o código já não vai caber na tela de vocês… Em compensação, esse episódio traz TRÊS novidades \o/ Hoje vamos programar e testar um somador de n-bits. Um somador que pode somar dois números com uma quantidade arbitrária de bits. A figura abaixo mostra exatamente a arquitetura que vamos implementar, é um somador “ripple-carry”:
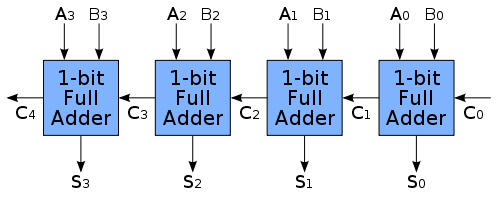
Pela figura já dá pra notar qual vai ser o conceito mais importante abordado nesse episódio: a modelagem hierárquica, usando componentes. Ou seja, nós vamos montar a arquitetura de um somador de n bits usando um componente mais simples já descrito, o nosso somador de 1 bit do episódio anterior. Claro, tem mais novidades, mas primeiro vamos ao código :)
library ieee;
use ieee.std_logic_1164.all;
entity nBitAdder is
Generic(nBits : integer := 8);
Port(
a : in std_logic_vector(nBits-1 downto 0);
b : in std_logic_vector(nBits-1 downto 0);
s : out std_logic_vector(nBits downto 0));
end nBitAdder;
architecture arch of nBitAdder is
component fullAdder is
Port(
a : in std_logic;
b : in std_logic;
cin : in std_logic;
s : out std_logic;
cout : out std_logic);
end component fullAdder;
for leftmost: fullAdder use entity work.fullAdder;
for rightmost: fullAdder use entity work.fullAdder;
constant N_BITS : integer := nBits;
signal sig_carryChain : array(1 to N_BITS-1) of std_logic;
begin
-- rightmost bit
rightmost: fullAdder
port map(
a => a(0),
b => b(0),
cin => '0',
s => s(0),
cout => sig_carryChain(1));
-- middle bits
middle: for i in 1 to N_BITS-2 generate
adder: fullAdder
port map(
a => a(i),
b => b(i),
cin => sig_carryChain(i),
s => s(i),
cout => sig_carryChain(i+1));
end generate middle;
-- leftmost bit
leftmost: fullAdder
port map(
a => a(N_BITS-1),
b => b(N_BITS-1),
cin => sig_carryChain(N_BITS-1),
s => s(N_BITS-1),
cout => s(N_BITS));
end arch;O nosso somador “nBitAdder” tem uma novidade em sua seção “entity”: É a declaração de parâmetros genéricos. Os parâmetros que estão declarados nessa seção “Generic” têm seu valor definido em tempo de síntese, e, portanto, nosso somador não pode ser configurado “ao vivo” :), ou seja, enquanto o circuito funciona. Diferentes valores para os parâmetros alteram a síntese, e geram diferentes blocos resultantes. Muitas coisas úteis no design de hardware são feitas com esse tipo de parametrização, mas por enquanto o que nós queremos é simples: ter um somador com entradas e saídas de tamanho genérico.
Agora, quanto à declaração das portas do nosso somador:
Port(
a : in std_logic_vector(nBits-1 downto 0);
b : in std_logic_vector(nBits-1 downto 0);
s : out std_logic_vector(nBits downto 0));Ele têm agora apenas duas entradas, que são os dois números a serem somados, cada um deles representado por nBits bits. O tipo de cada entrada é “std_logic_vector”, como nós já vimos no episódio anterior… A novidade é que a saída do nosso somador tem tamanho (nBits+1). Isso, claro, pois a soma de dois números com n bits pode gerar um número de no máximo n+1 bits :)
A seção architecture já traz a grande novidade logo no início: a declaração do componente que vamos utilizar, nesse caso um fullAdder. Essa modelagem que utiliza componentes mais simples para montar os mais complexos é o famoso “bottom-up”, e esse estilo “Lego-like” de modelagem de hardware é um dos mais utilizados. A declaração de um componente nada mais é do que uma CÓPIA da seção entity desse componente, trocando a palavra entity por component. Isso parece repetitivo, e é mesmo :P Existem maneiras de não repetir essa declaração, mas isso virá mais para frente no tutorial, por enquanto, usar component é a maneira mais simples de fazer design hierárquico…
A constante N_BITS não é necessária, eu só usei pra mostrar como se declara uma constante, não merece grandes explicações… Já na linha de baixo vem a declaração do sinal sig_carryChain. Como nós vamos utilizar n fullAdders, vamos precisar de n-1 fios pra interconectar as entradas e saídas de carry deles. É por isso que declaramos um array de sinais std_logic:
signal sig_carryChain : array(1 to N_BITS-1) of std_logic;Os índices do array vão de 1 até N_BITS-1, e portanto ele tem NBITS-1 elementos, onde cada elemento é do tipo std_logic.
Vamos então agora “montar” nosso LEGO, propriamente. Instanciamos o primeiro fullAdder, todos os outros serão instanciados de maneira semelhante.
rightmost: fullAdder
port map(
a => a(0),
b => b(0),
cin => '0',
s => s(0),
cout => sig_carryChain(1));O primeiro bit da soma (de índice 0) é o mais à direita, o bit menos significativo. Conectamos as entradas desse fullAdder com as primeiras entradas do nosso nBitAdder, a saída com a primeira saída e a saída de carry desse primeiro fullAdder é o primeiro sinal na nossa cadeia de carry. De forma semelhante instanciamos o último bit, o mais à esquerda. A única diferença é que a saída de carry do último fullAdder é ligada ao bit “extra” (índice N_BITS) da saída.
Para instanciar os bits “intermediários” nós precisamos de uma abordagem mais “flexível” :) Nós precisamos instanciar mais NBITS-2 fullAdders. É esse tipo de “repetição controlada” de uma estrutura que o “generate” oferece.
middle: for i in 1 to N_BITS-1 generate
adder: fullAdder
port map(
a => a(i),
b => b(i),
cin => sig_carryChain(i),
s => s(i),
cout => sig_carryChain(i+1));
end generate middle;Cada um dos somadores do meio tem suas entradas e saídas ligadas às entradas e saídas de índice correspondente na entidade de n bits. A entrada de carry vem do sinal correspondente na cadeia de carry, e a saída de carry vai pro próximo sinal da cadeia. Tudo se encaixa como deve :)
Em termos de estilo de código não temos nenhuma novidade! Mas o código de hoje mostra como seu usa comentários em VHDL. Em VHDL só existe comentário de uma linha: toda linha começando em (dois hífens consecutivos) é ignorada e considerada comentário.
Vamos então à parte emocionante do episódio: mostrar que o somador funciona, através de um testbench. Bem, dessa vez o código do próprio somador ficou grande, mas por incrível que pareça o código do testbench ficou relativamente pequeno, pois usamos os arrays que acabamos de aprender…
library ieee;
use ieee.std_logic_1164.all;
entity nBitAdder_testbench is
end nBitAdder_testbench;
architecture arch of nBitAdder_testbench is
component nBitAdder is
Generic(nBits : integer := 8);
Port(
a : in std_logic_vector(nBits-1 downto 0);
b : in std_logic_vector(nBits-1 downto 0);
s : out std_logic_vector(nBits downto 0));
end component nBitAdder;
for dut: nBitAdder use entity work.nBitAdder;
constant N_BITS : integer := 4;
signal sig_a : std_logic_vector(N_BITS-1 downto 0);
signal sig_b : std_logic_vector(N_BITS-1 downto 0);
signal sig_s : std_logic_vector(N_BITS downto 0);
type testInputArray is array(0 to 7) of std_logic_vector(N_BITS-1 downto 0);
type testOutputArray is array(0 to 7) of std_logic_vector(N_BITS downto 0);
constant testInputsA : testInputArray := (
"0000", "0001", "0100", "0101", "1000", "1001", "1100", "1101");
constant testInputsB : testInputArray := (
"1101", "1100", "1001", "1000", "0101", "0100", "0001", "0000");
constant testOutputs : testOutputArray := (
"01101", "01101", "01101", "01101", "01101", "01101", "01101", "01101");
begin
dut: nBitAdder
generic map(nBits => N_BITS)
port map(
a => sig_a,
b => sig_b,
s => sig_s);
tb: process
begin
for i in 0 to 7 loop
sig_a <= testInputsA(i);
sig_b <= testInputsB(i);
wait for 10 ns;
assert (sig_s = testOutputs(i)) report "fail" severity failure;
end loop;
assert false report "All tests passed." severity failure;
end process;
end arch;Pronto! Acabou! Funciona! Tá tudo bem agora.
Como sempre, pegue o código nesse pacote aqui: VHDL2, compile o testbench, veja que tudo funciona e confira as formas de ondo no GTWake, surfe nas ondas do testbench! :P Mais uma vez, o makefile empacotado junto com os arquivos VHDL vão te ajudar… Não se preocupe, tudo vai dar certo, pois esse tutorial tem o selo Entei de segurança:

