P = NP (or not)
It’s now becoming more and more fashionable to talk about Theory of Computation. One of Computer Science’s most famous unsolved problems made the headlines of The New York Times last Wednesday. Besides, this is also one of the Millenium Problems, and whoever solves it takes US$1.000.000 home. What unsolved problem am I talking about? It’s the P vs. NP problem.
The question is to know whether the set of problems easily verifiable (NP) equals the set of all problems easily solvable (P). One well-known problem that belongs to NP is the “15 puzzle”.
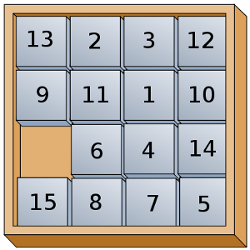
If you ever were a kid, than you played with this puzzle; but for those who weren’t kids I’ll explain… This puzzle comes assembled just like in the above picture, completely shuffled. Your goal is then very simple: rearrange the pieces into ascending order, of course without ripping the pieces off the board :P
But why is the “Fifteen Puzzle” an NP problem? Because if someone tells you a sequence of piece movements, it’s easy to verify that the sequence is indeed correct. All you need to do is perform the movements and check whether after the last movement all numbers are in order! But finding such a sequence, on the other hand, is much harder… You can try to program a computer to solve the Fifteen Puzzle (because computers are sooo powerful, aren’t they?). BUT, until today, nobody, none of the world’s most brilliant minds could find a solution smarter than BRUTE FORCE, which means trying all possible combinations of movements, one by one.
So it seems it’s impossible to solve the Fifteen Puzzle in a quicker way, and so it SEEMS that it doesn’t belong to P. Other two well-known games also have this characteristic: Sudoku and Minesweeper. Try to think for a while how easy it is to check a Sudoku game, and how hard it can be to solve…
The fact that no “quick” solution for these problems was found until now makes us believe that P and NP are diferrent, and there are problems which are easy to check but hard to solve. Still, there is no FORMAL PROOF of this inequality and, at the end of the day, this lack of quick solutions can just be a consequence of our (human) lack of intelligence and creativity.
If you still think all this crazy talk about P, NP, puzzles and minesweeper has nothing to do with “real life”, it’s time for some reflection :) One of the most famous problems that belongs to NP is studied by medicine and biology, it is protein folding.
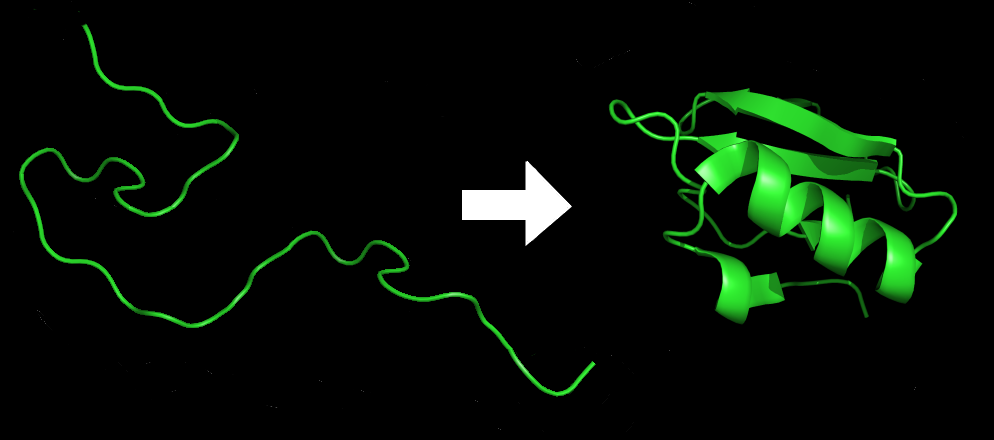
The problem of protein folding asks us to find out the aminoacid sequence of a protein, given only its 3D geometrical shape. In the last decades physicians and biochemists have found that misfolded proteins are the main cause of several diseases, and so a better understanding of how this folding process works could greatly improve the health of mankind.
I will probably write another post to talk a bit more about the unexpected implications of Theoretical Computer Science in daily life… But, for now, think twice before pointing a finger to a nerd and calling him/her self-centered. You think he is writing a program to solve Sudoku, but in fact he might be helping the world find the cure for cancer :P
